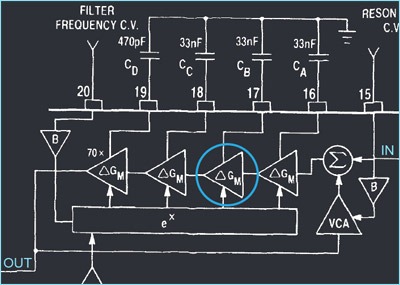
The following diagram from the CEM 3396 datasheet shows the VCF section:
The low pass filter consists of a series of four identical single pole sections (I circled one of them in blue).
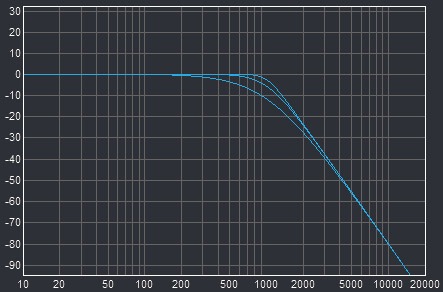
This graph shows the difference in the filter response compared to two other possible 4 pole filter designs:
All three curves have a 24 dB/octave slope on the right, but different transitions between the passband and the stopband. The curve with the sharpest transition is a Butterworth filter and the other curve close to that represents the response of two RLC circuits in series (just for theoretical comparison, not that such a circuit would be used in a synthesizer). The transition of the CEM filter is more gradual. In the couple of musical octaves above the cutoff frequency, the attenuation is closer to 18 than 24 dB/octave.
Filter resonance is accomplished by adding the inverted output signal back to the input. This works because each of the four poles causes a phase shift of –p/4 at the cutoff frequency, so the overall phase shift is -p and inverting the signal brings it in phase with the input, reinforcing this particular frequency. The amount of resonance is controlled by varying the amplification of the feedback signal.
This diagram shows how the frequency response of a simple digital filter is affected by the resonance parameter (the five curves correspond to no resonance and four different levels of resonance):
Four single pole filters in series and with a feedback loop to generate resonance have a different frequency response:
One major difference between the two graphs is that the last one shows that the passband is increasingly attenuated as the resonance increases.
How close is this ‘ideal’ CEM 3396 filter response to the actual response?
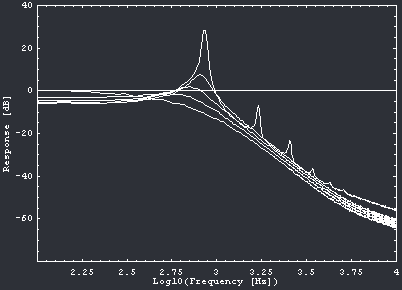
Here are filter measurements from a Matrix 1000:
We can ignore that at the right end of this graph the steepness of the curve decreases: This is only due to the noise floor.
Comparing the last two graphs we can note some major differences:
- At maximum resonance, the spike in the first graph (the theoretical filter response) seems narrower. It’s unclear whether this is real or just due to different curve interpolation when drawing the graph (the measured response has lower frequency resolution because it’s the result of a discrete Fourier transform rather than the plot of a theoretical formula).
- The frequency response measured at maximum resonance shows a dramatic difference: extra spikes along the curve! These spikes have center frequencies corresponding to harmonics of the filter cutoff frequency. They are caused by the non-linear behavior of the filter circuit.
(The extra spikes are not really part of the frequency response, but they appear in it as an artifact of the way I measured it. The graph is actually a plot of the spectrum of white noise processed by the filter, and this is identical to the frequency response of the filter if the filter is 100% linear, but if the filter is not completely linear then the measured spectrum will also show the effects of the nonlinearities in addition to the frequency response.) - The right half of the Matrix 1000 filter graph shows a series of parallel downward lines rather than a single line like in the theoretical case. This means that the CEM 3396 amplifies the signal at higher resonance settings to correct most of the passband attenuation caused by the feedback loop.
In the following graph, the same Matrix 1000 filter measurements have been adjusted (by adding an offset to each curve) to “undo” the gain correction performed by the CEM 3396 filter:
Now the graph is very similar to the predicted ideal behavior of a series of four single pole filters with a feedback loop, except for the extra spikes at self-oscillation.
A software implementation of the filter will need to at least emulate the non-linearities that introduce extra harmonics (especially noticeable at high levels of resonance) as they are a major factor of why analog filters are often perceived as warmer and “fatter” compared to common and simpler digital filter designs.
TechnoTAG: ZGZN95CJJZEK